A Chi-square test is performed to determine if there is a difference between the theoretical population parameter and the observed data.
- Chi-square test is a non-parametric test where the data is not assumed to be normally distributed but is distributed in a chi-square fashion.
- It allows the researcher to test factors like a number of factors like the goodness of fit, the significance of population variance, and the homogeneity or difference in population variance.
- This test is commonly used to determine if a random sample is drawn from a population with mean µ and the variance σ2.
Interesting Science Videos
Chi-square test uses
Chi-square test is performed for various purposes, some of which are:
- This method is commonly used by researchers to determine the differences between different categorical variables in a population.
- A Chi-square test can also be used as a test for goodness of fit. It enables us to observe how well the theoretical distribution fits the observed distribution.
- It also works as a test of independence where it enables the researcher to determine if two attributes of a population are associated or not.
Chi-square test formula
Chi-square test is symbolically written as χ2 and the formula of chi-square for comparing variance is given as:
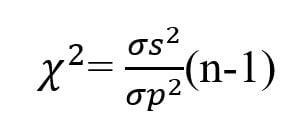
where σs2 is the variance of the sample,
σp2 is the variance of the sample.
Similarly, when chi-square is used as a non-parametric test for testing the goodness of fit or for testing the independence, the following formula is used:
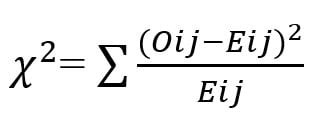
Where Oij is the observed frequency of the cell in the ith row and jth column,
Eij is the expected frequency of the cell in the ith row and jth column.
Conditions for the chi-square test
For the chi-square test to be performed, the following conditions are to be satisfied:
- The observations are to be recorded and collected on a random basis.
- The items in the samples should all be independent.
- The frequencies of data in a group should not be less than 10. Under such conditions, regrouping of items should be done by combining frequencies.
- The total number of individual items in the sample should also be reasonably large, about 50 or more.
- The constraints in the frequencies should be linear and not containing squares or higher powers.
Chi-square distribution
- Chi-square distribution in statistics is the distribution of a sum of the squares of independent normal random variables.
- This distribution is a special case of the gamma distribution and is one of the most commonly used distributions in statistics.
- This distribution is used for the chi-square test for testing the goodness of fit or testing the independence.
- Chi-square distribution is a part of the t-distribution, F-distribution used for t-tests, and ANOVA.
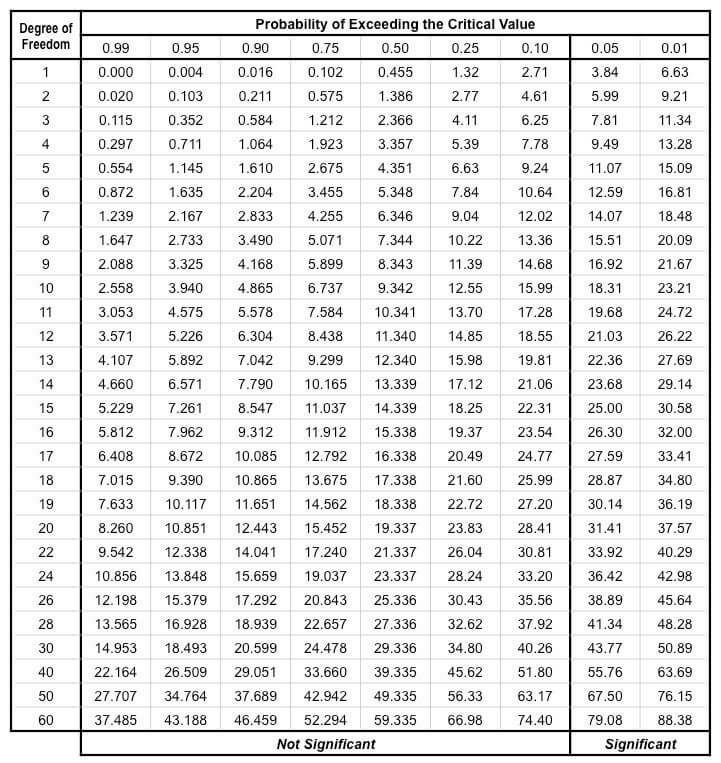
Chi-square table
The following is the chi-square distribution table:
Chi-square test of independence
- When the chi-square test is used as a test of independence, it allows the researcher to test whether the two attributes being tested are associated or not.
- For this test, a null and alternative hypothesis is formulated where the null hypothesis is that the two attributes are not associated, and the alternative hypothesis is that the attributes are associated.
- From the given data, the expected frequencies are then calculated, followed by the calculation of chi-square value.
- Based on the calculated value of chi-square, either the null or alternative hypothesis is accepted.
- Here, if the calculated value of chi-square is less than the value in the table at the given level of significance, the null hypothesis is accepted, indicating that there is no relationship between the two attributes.
- However, if the calculated value of chi-square is found to be higher than the value in the table, the alternative hypothesis is accepted, indicating that there is a relationship between the two attributes.
- The chi-square test only established the existence of a relationship but not the degree of the relationship or its form.
Chi-square test of goodness of fit
- Chi-square test is performed as a test of goodness of fit, which helps the researcher to compare the theoretical distribution with the observed distribution.
- When the calculated value of chi-square is found to be less than the table value at a certain level of significance, the fit between the data is considered to be good.
- A good fit indicates that the variation between the observed and expected frequencies is due to fluctuations during sampling.
- However, if the calculated value of chi-square is greater than the table value, the fit is considered not to be as good.
Chi-square test examples
- A chi-square test performed to determine if a new medication is effective against fever or not is an example of a chi-square test as the test of independence to determine the relationship between medicine and fever.
- Another example of the chi-square test is the testing of some genetic theory that claims that children having one parent of blood type A and the other of blood type B will always have the blood group as one of three types, A, AB, B, and that the proportion of three types will on an average be as 1: 2: 1. On the basis of expected and observed outcomes, the goodness of fit of the hypothesis can be determined.
Chi-square test applications
- A Chi-square test is used in cryptanalysis to determine the distribution of plain text and decrypted ciphertext.
- Similarly, it is also used in bioinformatics to determine the distribution of different genes like disease genes and other important genes.
- A Chi-square test is performed by various researchers of different fields to test the minor or major hypothesis.
References and Sources
- R. Kothari (1990) Research Methodology. Vishwa Prakasan. India.
- 2% – https://www.yourarticlelibrary.com/project-reports/chi-square-test/chi-square-test-meaning-applications-and-uses-statistics/92394
- 2% – https://www.slideshare.net/anandsplash007/chi-square-rm
- 2% – https://en.wikipedia.org/wiki/Chi-squared_distribution
- 1% – https://www.vedantu.com/maths/non-parametric-test
- 1% – https://www.thoughtco.com/null-hypothesis-vs-alternative-hypothesis-3126413
- 1% – https://www.statisticssolutions.com/chi-square-goodness-of-fit-test/
- 1% – https://www.slideshare.net/KishanKasundra1/goodness-of-fit-test
- 1% – https://www.investopedia.com/ask/answers/073115/what-assumptions-are-made-when-conducting-ttest.asp
- 1% – https://us.sagepub.com/sites/default/files/upm-binaries/82020_Chapter_11.pdf
- 1% – https://us.sagepub.com/sites/default/files/upm-assets/82020_book_item_82020.pdf
- 1% – https://support.sas.com/resources/papers/proceedings/proceedings/sugi31/200-31.pdf
- 1% – https://openstax.org/books/introductory-statistics/pages/13-2-the-f-distribution-and-the-f-ratio
- 1% – https://link.springer.com/referenceworkentry/10.1007/978-0-387-32833-1_400
- 1% – https://en.wikipedia.org/wiki/Chi-square_distribution
- 1% – http://www.self.gutenberg.org/articles/Chi-squared_test
- 1% – http://www.davidmlane.com/hyperstat/B155367.html
- 1% – http://maxwell.ucsc.edu/~drip/133/ch4.pdf
- <1% – https://www.wisdomjobs.com/e-university/research-methodology-tutorial-355/chi-square-as-a-non-parametric-test-11546.html
- <1% – https://www.thoughtco.com/chi-square-goodness-of-fit-test-example-3126382
- <1% – https://www.statisticssolutions.com/chi-square-test/
- <1% – https://www.slideshare.net/parth241989/chi-square-test-16093013
- <1% – https://byjus.com/chi-square-formula/
- <1% – http://learntech.uwe.ac.uk/da/Default.aspx?pageid=1440
- <1% – http://dataanalyticsedge.com/2016/12/23/chisquare-test-different-types-and-its-application-using-r/
